사례3.
|
교통국장은 교통교육의 효과를 알아보기 위하여 교육을 이수한 사람과 그렇지 않은 사람과의 법규위반여부를 조사하였다. 만약, 교통교육의 준법운전에 대한 효과가 없다면 교통교육을 폐지하거나 축소할 방침이다. 문3-1. 자료를 이용하여 2X2교차표를 만들고 기대빈도와 관측빈도를 구할 것. 문3-2. 여러분이 교통국장이라면 교통안전교육을 존속, 강화하겠는가 아니면 폐지, 축소하겠는가? 95% 신뢰수준에서 검증할 것. (여기서 0은 교육미이수를 한 자, 그리고 교통법규위반이 없는 자이며 1은 교육 이수자, 그리고 법규위반경험이 있는 자를 의미한다.) |
<문제의 소재>
교통교육 이수 여부에 따라 교통법규위반 여부가 영향을 받는지 알아보려는 것 이므로, 어떤 모집단에서 어떤 속성을 가진 것의 비율과 가지고 있지 않는 것의 비율에 따라 또 다른 속성을 가진 비율과 그렇지 않은 비율 간의 상관관계 여부 를 조사하는 카이스퀘어 검정을 하면 된다.
<검정의 원리>
카이스퀘어 검정은 모집단에서 각각의 속성이 나타나는 비율에 따른 기대빈도와 실체로 관측된 실제빈도간의 차이를 비교 검정하여 각각의 속성이 독립적인지 연 관성이 있는지 알아본다.
문제 3에서는 교통교육의 이수여부와 교통법규위반사이 의 기대빈도와 실제로 관측된 관측빈도 사이의 상관관계를 조사하는 것이다.
<문제의 해결>
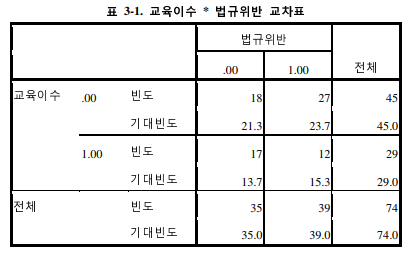
<표 3-1> 은 교차분석한 결과인 2 X 2 교차표를 나타낸다. 각각의 속성의 분포 비율과 그에 따른 기대빈도, 실제로 관측된 관측빈도와 각 열과 행의 합을 나타 낸 2X2 교차표이다.
기대빈도가 도출되는 과정은 간단하다. 첫 행, 첫 열의 실제 빈도인 18과 기대빈도 21.3이 나온 과정을 살펴보면, 전체 74개의 표본 중에 법 규위반을 하지 않은 자의 비율은 35/74 에 해당하고 다시 전체 74개의 표본 중 에 교육이수를 받지 않은 자의 비율은 45/74에 해당한다.
따라서 교통법규위반 여부와 교통교육이수 여부가 독립적이라면 교통법규를 위반하지 않고 교육을 이 수받지 않은 자의 비율은 (35/74)*(45/74) 가 될 것이고 이에 따른 기대빈도는 21.3 이 된다.
<표 3-2>는 카이스퀘어 검정 결과이다. 카이스퀘어 값은 2.453임을 알 수 있다. 이는
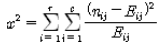
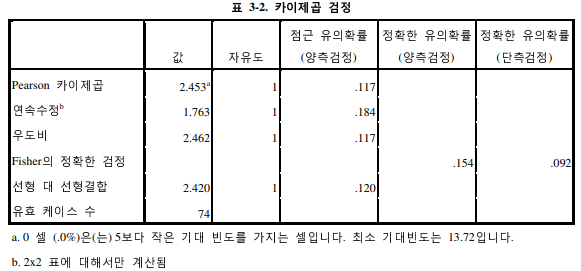
식을 이용한다.
카이스퀘어 값을 구한 다음에는 자유도를 구해서 카이스퀘어 분할표의 유의도를 파악한다. 자유도는 (2-1)(2-1)=1이 된다. 카이스퀘어 표에 의거해 귀무가설(교통교육이수여부와 교통법규위반여부는 독립적이다.)의 귀각여부를 결정한다.
문제 3의 경우, 자유도는 1, 카으스퀘어 값은 2.453이므로 유의수준(P)은 0.117 정도가 된다. 따라서 신뢰수준 95%에서 P=0.117 > 0.05 이므로 귀무가설을 채택한다. 즉, 교통교육이수여부와 교통법규위 반여부는 독립적이다.
<결론>
교통교육이수여부와 교통법규위반여부는 그 연관성을 인정할 수 없이 독립적 이므로(신뢰수준 95%) 교통국장은 교통안전교육을 축소하는 한편 교통법규위반을 줄이기 위한 다른 방법을 모색해야 한다.
'경찰학(警察學)' 카테고리의 다른 글
| 범죄자 프로파일링의 이론적 토대 (0) | 2019.04.22 |
|---|---|
| 범죄자 프로파일링의 개념 (0) | 2019.04.19 |
| [교통안전규제론] 사례 해결 - 4 (0) | 2019.04.09 |
| [교통안전규제론] 사례 해결 - 2 (0) | 2019.04.09 |
| 경찰실무종합(2018년 경찰공제회) - 각론 두문자 (1) | 2019.04.02 |
