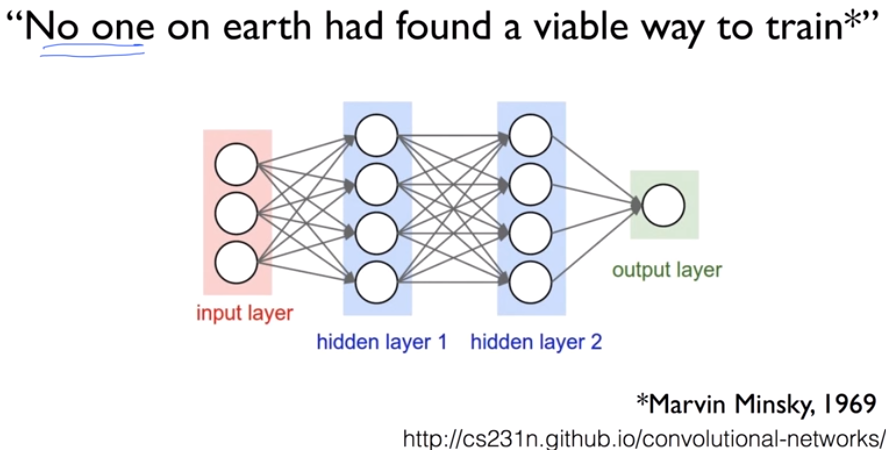
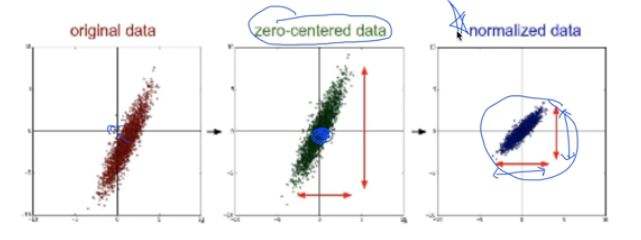
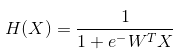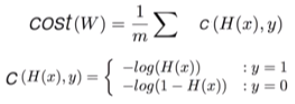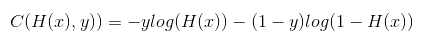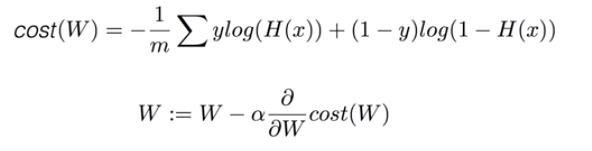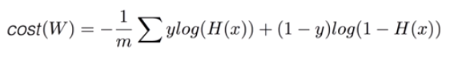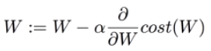※ 김성훈 교수님의 [모두를 위한 딥러닝] 강의 정리
- https://www.youtube.com/watch?reload=9&v=BS6O0zOGX4E&feature=youtu.be&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm&fbclid=IwAR07UnOxQEOxSKkH6bQ8PzYj2vDop_J0Pbzkg3IVQeQ_zTKcXdNOwaSf_k0
- 참고자료 : Andrew Ng's ML class
1) https://class.coursera.org/ml-003/lecture
2) http://www.holehouse.org/mlcass/ (note)
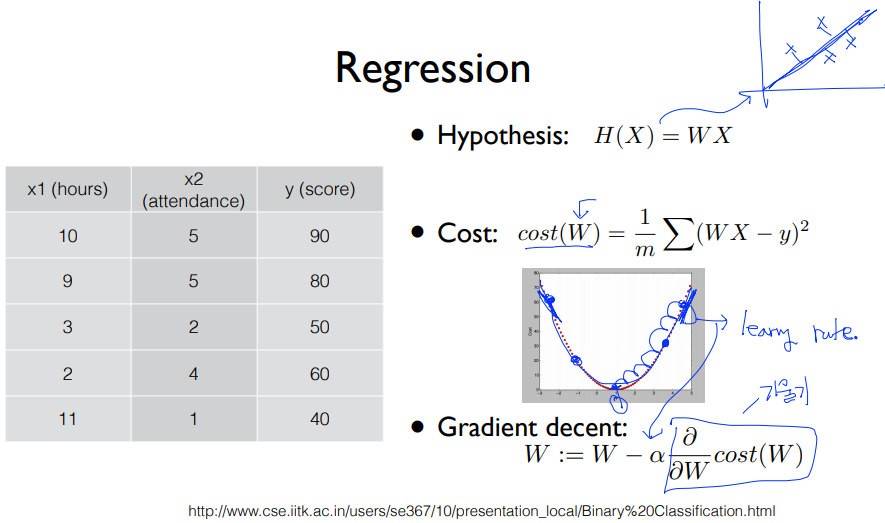
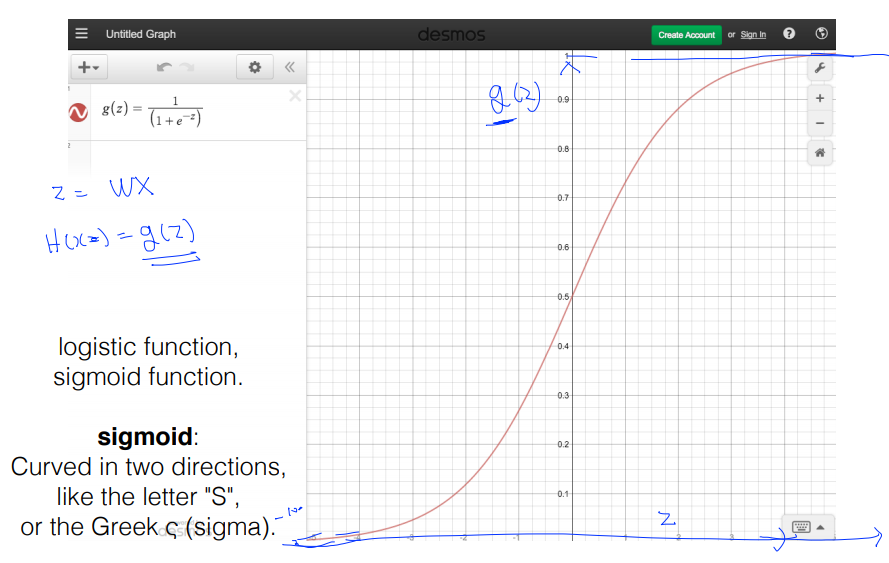
1. (Linear) Hypothesis and cost function
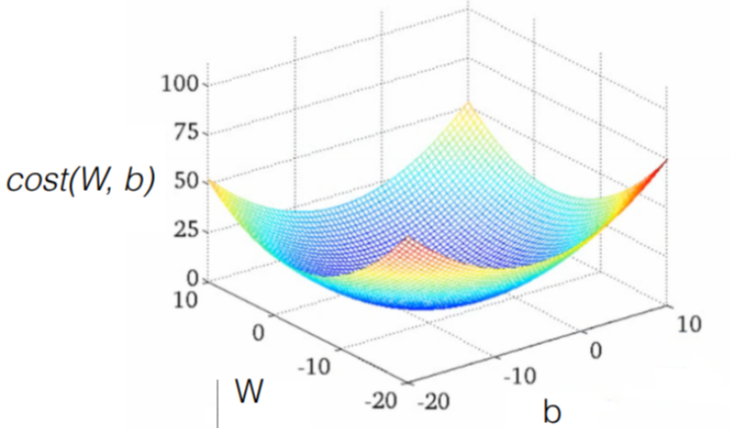
* Hypothesis : H(x) = Wx + b
* Cost function(W,b) = ( H(x) - y ) ^ 2 // How fit the line to our (training) data
* Goal = Minimize cost
2. How to minimize cost
* 학습 : W,b 값을 조정하여 cost 값을 최소화 하는 과정
(1) 그래프 생성
import tensorflow as tf
# X and Y data
x_train = [1 , 2 , 3 ]
y_train = [1 , 2 , 3 ]
# Try to find values for W and b to compute y_data = x_data * W + b
# We know that W should be 1 and b should be 0
# But let TensorFlow figure it out
W = tf.Variable(tf.random_normal([1 ]), name = " weight"
b = tf.Variable(tf.random_normal([1 ]), name = " bias"
# Our hypothesis XW+b
hypothesis = x_train * W + b
# cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - y_train))
* GradientDescent : 학습
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)
train = optimizer.minimize(cost)
(2) 세션 실행 : 데이터 입력 및 그래프 실행
# Launch the graph in a session.
sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
# Fit the line
for step in range (2001 ):
sess.run(train)
if step % 20 == 0 :
print (step, sess.run(cost), sess.run(W), sess.run(b))
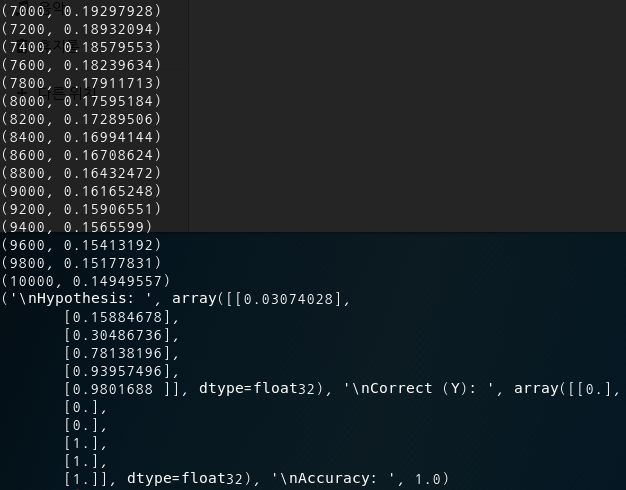
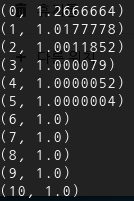
(3) 그래프 업데이트 및 결과값 반환 : 학습에 의해 cost를 최소화하는 W, b 값 추론
...
(0, 3.5240757, array([2.1286771], dtype=float32), array([-0.8523567], dtype=float32))
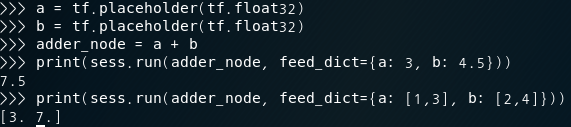
3. How to minimize cost (placeholder 이용) // 에러..
import tensorflow as tf
W = tf.Variable(tf.random_normal([1 ]), name = ' weight'
b = tf.Variable(tf.random_normal([1 ]), name = ' bias'
X= tf.placeholder(tf.float32, shape=[None])
Y= tf.placeholder(tf.float32, shape=[None] )
# Our hypothesis XW+b
hypothesis = X * W + b
# cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y)
# Minimize
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01 )
train = optimizer.minimize(cost)
# Launch the graph in a session.
sess = tf.Session()
# Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
# Fit the line with new training data
for step in range (2001 ):
cost_val, W_val, b_val, _ = sess.run([cost, W, b, train], feed_dict={X: [1, 2, 3, 4, 5], Y: [2.1, 3.1, 4.1, 5.1, 6.1])
if step % 20 == 0 :
print (step, cost_val, W_val, b_val)
(0, 1.2035878, array([1.0696986], dtype=float32), array([0.01276637], dtype=float32))